Gosper island
is a geometric object that clearly demonstrates the necessity of
considering fractal dimensions.
We construct it as follows: let start with the hexagon
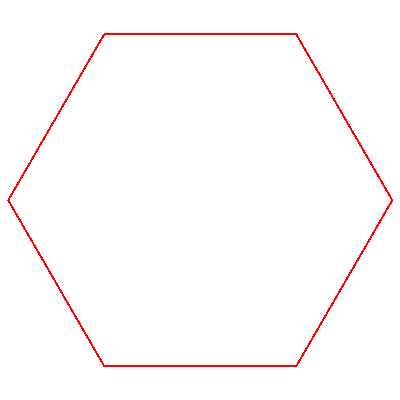
On the first step we replace each side with the broken line consisting of three intervals:
and obtain
Again we replace every interval in the boundary by similar broken line:
and obtain
And so on....
In the limit we obtain
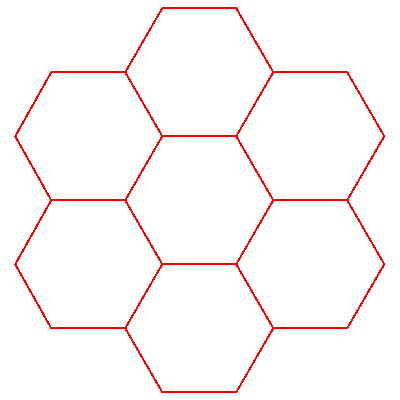
The Gosper islands can be used to tile the plane. Let us consider 7 adjacent islands.
We have:
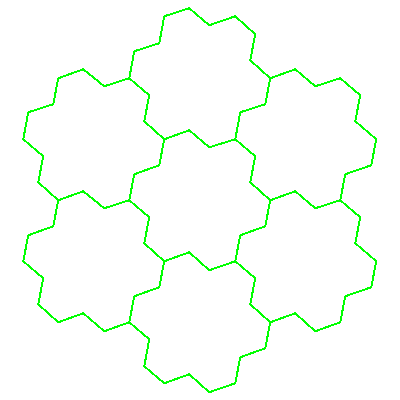
And in the limit we obtain:
We see that the large island (consisting of 7 smaller) is similar to the each of the smaller islands. The similarity factor is 71/2
since the area of large island is obviously 7 times the area of small island. Surprisingly, the perimeter of the large island
is 3 times the perimeter of of the small island (it is perfectly visible at early construction stages). We remember from school
that it should be exactly 71/2 ~ 2.645751311 times larger (for example if we double the side of the square, then its area
increases 4 times). Have we just found a contradiction in mathematics ?
Not really. The boundary of the island is not a curve in the standard meaning of the word, i.e., it is not one dimensional.
Its dimension d is such a number that (71/2)d = 3 , i.e., d = 2 ln(3)/ln(7) ~1.129150068 . The boundary of Gosper Island
is of fractal dimension larger than 1 but smaller than 2.
We construct it as follows: let start with the hexagon
On the first step we replace each side with the broken line consisting of three intervals:
and obtainAgain we replace every interval in the boundary by similar broken line:
and obtain And so on....In the limit we obtain
The Gosper islands can be used to tile the plane. Let us consider 7 adjacent islands.
We have:
And in the limit we obtain:
We see that the large island (consisting of 7 smaller) is similar to the each of the smaller islands. The similarity factor is 71/2
since the area of large island is obviously 7 times the area of small island. Surprisingly, the perimeter of the large island
is 3 times the perimeter of of the small island (it is perfectly visible at early construction stages). We remember from school
that it should be exactly 71/2 ~ 2.645751311 times larger (for example if we double the side of the square, then its area
increases 4 times). Have we just found a contradiction in mathematics ?
Not really. The boundary of the island is not a curve in the standard meaning of the word, i.e., it is not one dimensional.
Its dimension d is such a number that (71/2)d = 3 , i.e., d = 2 ln(3)/ln(7) ~1.129150068 . The boundary of Gosper Island
is of fractal dimension larger than 1 but smaller than 2.